So,How Do You Solve The Megaminx?

Well, I know personally that having the megaminx solved can be a special feat. When I was first looking at the this alternative to the rubik's cube I was thinking to myself there is no way that I will be able to figure out how to do this but. Like any thing else with time and patience and effort I figured it could be done with enough tweaking and consistency.
I decided to make this website for those who want to learn how to solve a megaminx. The best place to start would be to of course buy or order a megaminx and then start developing your megaminx cube into a completed shape.
Then after doing that I recommend that you go to the video guide that I've found for you to start actually plugging away at this complex looking cube.
Step 1: Visit the video guide
More About The Megaminx
For those of you who may be wondering about what exactly the megaminx is, it is basically a rubik's cube that has more sides and shapes but some of the core principles of this cube is the same as the rubik's
I decided to make this website for those who want to learn how to solve a megaminx. The best place to start would be to of course buy or order a megaminx and then start developing your megaminx cube into a completed shape.
Then after doing that I recommend that you go to the video guide that I've found for you to start actually plugging away at this complex looking cube.
Step 1: Visit the video guide
More About The Megaminx
For those of you who may be wondering about what exactly the megaminx is, it is basically a rubik's cube that has more sides and shapes but some of the core principles of this cube is the same as the rubik's
A Dodecahedron?

There is a seemingly natural progression from cube to Dodecahedron.But in reality this cube can pretty much be the exact same thing as a rubik's.
Alot of people who have decided to make a variation of the rubik's one after another.
To quote from Cubic Circular, Issue 3&4, (David Singmaster, Spring&Summer 1982): "The Magic Dodecahedron has been contemplated for some time. So far I have seen photos or models from: Ben Halpern (USA), Boris Horvat (Yugoslavia), Barry Lockwood (UK) and Miklós Kristóf (Hungary), while Kersten Meier (Germany) sent plans in early 1981.
I have heard that Christoph Bandelow and Doctor Moll (Germany) have patents and that Mario Ouellette and Luc Robillard (Canada) have both found mechanisms.
The Hungarian version is notable as being in production ... and as having planes closer to the centre so each face has a star pattern."
"Uwe Mèffert has bought the Halpern and Meier rights, which were both filed on the same day about a month before Kristóf. However there is an unresolved dispute over the extent of overlap in designs."
Alot of people who have decided to make a variation of the rubik's one after another.
To quote from Cubic Circular, Issue 3&4, (David Singmaster, Spring&Summer 1982): "The Magic Dodecahedron has been contemplated for some time. So far I have seen photos or models from: Ben Halpern (USA), Boris Horvat (Yugoslavia), Barry Lockwood (UK) and Miklós Kristóf (Hungary), while Kersten Meier (Germany) sent plans in early 1981.
I have heard that Christoph Bandelow and Doctor Moll (Germany) have patents and that Mario Ouellette and Luc Robillard (Canada) have both found mechanisms.
The Hungarian version is notable as being in production ... and as having planes closer to the centre so each face has a star pattern."
"Uwe Mèffert has bought the Halpern and Meier rights, which were both filed on the same day about a month before Kristóf. However there is an unresolved dispute over the extent of overlap in designs."
Many Different Versions

As stated above there has been several versions of the megaminx and the rubiks. The regular megaminx has 6 to 12 other colors.The top layers of the cube are thin so this makes the edge of the pieces have some width in them.
Have you ever heard of the supernova? this cube in particular has 12 colors with much thicker face sections which meet in the center edge.
Have you heard of the Alexander Star? this about the same as the megaminx except without the corners or centres,and also the impossiball wich is like the megaminx without edges or centres.
Have you ever heard of the supernova? this cube in particular has 12 colors with much thicker face sections which meet in the center edge.
Have you heard of the Alexander Star? this about the same as the megaminx except without the corners or centres,and also the impossiball wich is like the megaminx without edges or centres.
The Number Of Positions

Impossiball
It is a total of 30 edge pieces with 2 variations with each sections,and 20 corner pieces with 3 orientations,giving a maximum of 30!·20!·230·320 positions. The main cannot be reached because
- only even permutations of edges are possible (2)
- only even permutations of corners are possible (2)
- only and even number of flipped edges are possible (2)
- the total twist of the corners is fixed (3)
Lets say if online 6 colors are being used, then 15 pieces won't be different from the other which can then divided by 214 (not 215 since only an even number of swaps are possible) which gives ,144,385,775,971,883,979,645,753,925,393,402,415,081,061,792,664,780,800,000,000,000 or 6.1·1063 positions. Even it seems alot to do then I can honestly say that it is not that much harder then the rubik's cube. I know looking at it for the first time you would probably disagree.
Solving The Megaminx
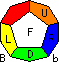
Megaminx R
Allow L,U, R,F Be the three adjancent (Up, Right and Front) simply meaning that U, R, F that circle around in a vertex pattern.Let D be the other facing right next to both F and R.Clockwise 1/5 twists twists of a face are denoted by the correct letter.anti-clockwise 1/5 twists by U', R', F' or D'.
In the problem solver steps below, You can see that the D face is normally not solved.
We can give the positions of the edge pieces by using two letters, for the complete example U,F is the side that stays in both the U and F faces. Similarly, corners are denoted by three letters as they lie in three faces.
In the problem solver steps below, You can see that the D face is normally not solved.
We can give the positions of the edge pieces by using two letters, for the complete example U,F is the side that stays in both the U and F faces. Similarly, corners are denoted by three letters as they lie in three faces.
Megaminx Phase 1

Solve everything but the final face
- Did you know that you can solve with only one face. This can be an easy to do follow system doesn't need to be told in much detail considering the simplicity. let that U be one of the ony facings.
- Solve the corners of the U face using the examples Below:
1.Locate the corner the belongs to the U face.
2. Grip the puzzle so that the corner belongs to the URF, and face D is solved.
3. Use any turns that do not mess with the already completeled pieces to place the corner at RDF.
4.You can also use one of the following pieces for the corner:
RDF->URF: R'D'R
FRD->URF: FDF'
DFR->URF: R'DR FD'D'F'
Most of these sequences do not mess with the FR edge piece and the D layer, but nothing else except for the corner. The sequences change only in the same area of the corner. If you use the wrong sequence for your type of cube you are building then, the URF corner can be altered in place by R'DR FDF'.
5. Repeat 1-4 till done. If needed you should use this strategy to displace a corner that you need somewhere else.
Phase 1 Continued

- Place all edges that are not yet solved in an adjacent to the solved corners. This is similar to placing the corners, except that you use the following sequences to place them:
DR->FR: DFD'F' D' R'DR
FD->FR: D'R'DR D FD'F'
These sequences only alter the D layer, but nothing else except for the edge. If an edge is in position but flipped, then displace it by placing any other edge piece there with one of the sequences, and then insert the edge piece in the correct orientation. - Make sure you do steps b-c to face in turn, until only one unsolved face is left.
Phase 2: Orient the edges of the final face.

The edges are flipped in pairs. It is impossible to have only one edge upside down.
- Hold the puzzle so that the unsolved face is D, one edge to be flipped is at DR, and another is either at DL or DF.
- Do one of the following sequences to flips the edges:
To flip DF, DR, do R D F D' F' R'
To flip DL, DR, do R F D F' D' R' - Repeat the above if necessary.
- Rotate D to place as many edges as possible in their correct places. If, like Alexander's Star, your megaminx has only 6 colours, you might find that the edges are in an odd permutation. In this case you will have to swap any two identical edges elsewhere on the puzzle and try solving it again.
- Hold the puzzle so that you can use one of the following sequences to solve it:
1. DR->DF->DL->DR: R D R' D R D'D' R'
2. DR->DL->DF->DR: R DD R' D' R D' R'
3. DR->DF->DB->DR: R D R' DD R DD R'
4. DR->DB->DF->DR: R D'D' R' D'D' R D' R'
5. DR-DB, DF-DL: R D R' D R D' R' DD R DD R'
- Hold the puzzle so that you can use one of the following sequences to solve it:
1. DFR->DLF->DBL->DFR: RUR' D RU'R' D RUR' D'D'RU'R'
2. DFR->DBL->DLF->DFR: RUR' DD RU'R' D' RUR' D' RU'R'
3. DFR->DLF->DbB->DFR: RUR' D RU'R' DD RUR' DD RU'R'
4. DFR->DbB->DLF->DFR: RUR' D'D'RU'R' D'D'RUR' D' RU'R'
5. DFR-DbB, DLF-DBL: RUR' D RU'R' D RUR' D' RU'R' DD RUR' DD RU'R'
Note the similarity between these sequences and those of phase 3.
- Hold the puzzle so that the DFR corner needs to be twisted anti-clockwise. If there is no such corner, then put a different twisted corner there.
- To turn DFR anti-clockwise, and another clockwise, do one of these:
1. DFR->RDF, DLF->LFD: RU'R'F'U'F D F'UFRUR' D'
2. DFR->RDF, DBL->BLD: RU'R'F'U'F DD F'UFRUR' D'D'
3. DFR->RDF, DbB->bBD: RU'R'F'U'F D'D' F'UFRUR' DD
4. DFR->RDF, DFb->FbD: RU'R'F'U'F D' F'UFRUR' D - Repeat the above until all corners are correct.

